k近邻(k-nearest neighbor)是一种基本的分类和回归方法。分类时,对新的实例,根据其k个最近邻的训练实例的类别,通过多数表决等方式进行预测。因此,k近邻法不具有显式的学习过程。
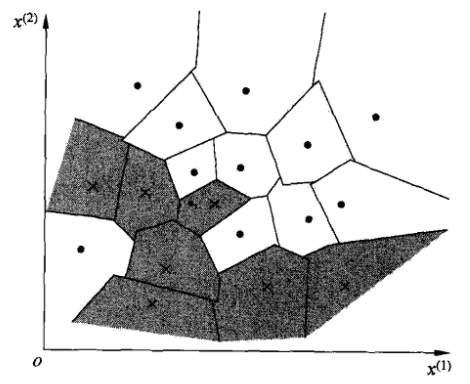
k近邻实际上利用训练数据集对特征向量空间进行划分,并作为其分类的模型。
k近邻
图片来自《统计学习方法》。
三要素
k近邻是一个比较简单的机器学习算法,k近邻的三要素是:
- k值的选择
- 距离度量
- 分类决策规则
给定训练集,对于新的输入,在训练集中找到与该实例最临近的k个实例,这k个实例的多数属于某一类,则认为该实例属于这个类。
算法

当k=1时,成为最近邻法。
k近邻模型
模型
将特征空间划分为子空间,确定空间中的每个点所属的类。
度量距离
$x_{i}$与$x_{j}$的距离$L_{p}$:
这个距离,又称为范数。
- 当$p=1$时,成为曼哈顿距离;
- 当$p=2$时,称为欧氏距离;
- 当$p=\infty$时,它是各个坐标距离的最大值;
k值的选择
- k较小时,近似误差会减小,但估计误差会增大,结果对近邻的点敏感,如果近邻有噪声会影响很大;
- k较大时,可以减小估计误差,增大近似误差,模型也相对更简单;
分类决策的规则
多数表决
