今天开始写SVM，博主对SVM的理解其实也是比较有限，但是我认为SVM的推理是一道坎，对机器学习热爱的话就一定要跨过这道坎。博文内容来自我之前学习机器学习数学基石的课程，SVM部分总共分为三部曲，本文是第一部分—凸优化问题。
现在是3月9日凌晨2点，今晚一回家小睡了一会醒来居然快12点了，现在精神异常亢奋，同时大脑状态还停留在3月8号，so补一句女神节快乐！

本文是SVM三部曲中的第一篇。知识点和文章结构是学习了稀牛学院数学基石课程后的总结。
SVM三部曲之凸优化问题
 SVM三部曲之凸优化对偶
 SVM三部曲之SVM终极推导

直接开始进入正题吧！

一般优化问题

无约束优化问题

假设自变量为矢量，无优化优化问题的数学形式可以表达为：

$\min{f(x)},x \in R^{n}$

这时候，我们通常可以使用的揭发有：

直接法：令梯度等于0，求得驻点，必要时求Hessaian矩阵再进一步判断；
迭代法：如梯度下降法、牛顿法、拟牛顿法

一般约束优化问题

约束优化问题的一般形式可以表示为：

$minimize \quad f_{0}(x) \\ \begin{align*} subject \ to: \ & f_{i}(x) \le 0, \quad for \ i=1,2,...,m \\ & h_{i}(x) = 0 \quad for \ i=1,2,...,p \end{align*}$

其中可行域为，满足$f(x)$定义域和约束条件的$x$的集合。$f_{j}(x)=0$表明不等式约束被激活。

举个例子，假设有以下约束优化问题：

$minimize \quad f_{0}(x)=x_{1}^{2}+x_{2}^{2}-4x_{1}+4=(x_{1}-2)^{2}+x_{2}^{2} \\ \begin{align*} subject \ to: \ & c_{1}(x)=x_{1}-2x_{2}+6 \ge 0 \\ & c_{2}(x)=-x_{1}^{2}+x_{2}-1 \ge 0 \\ & c_{3}(x)=x_{1} \ge 0 \\ & c_{4}(x)=x_{2} \ge 0 \end{align*}$

可行域在坐标系统中可以表示为下图：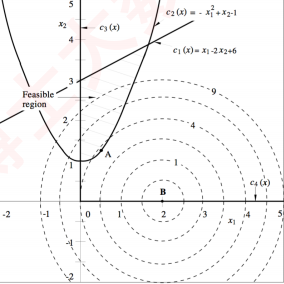

凸集和凸函数基础

仿射集和凸集

仿射集：如果一个集合是$C \in R^{n}$是仿射的，则$C$中两点间的直线也在$C$中，例如 $x=\theta x_{1}+(1-\theta)x_{2} \in C,\theta \ in \ R$
凸集：如果一个集合是$C \in R^{n}$是凸的，则对于任意的$x,y \in C$，有 $\theta x + (1-\theta)y \in C, \ 0 \le \ \theta \ \le \ 1$ 下图中，第一个集合就是一个凸集，二三两个为非凸集，因为存在域内两点间直线上的点不在集合中的情形。

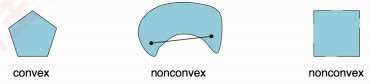
凸集的性质

凸集的交集市凸集
凸集的并集不一定是凸集

凸函数

凸函数的定义是：一个函数$f$被称为凸函数，则$f$的定义域为凸集，同时对于定义域中的任何两个点$x,y$和参数$0\le\theta\le 1$，有 $f(\theta x + (1-\theta)y)\le\theta f(x)+(1-\theta)f(y)$，如果不好理解的话，可以看下图的几何解释。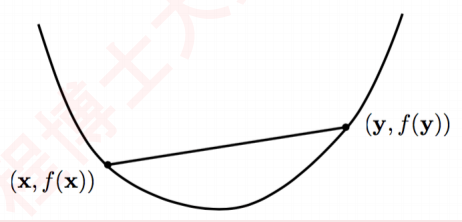

凸函数的一阶二阶条件

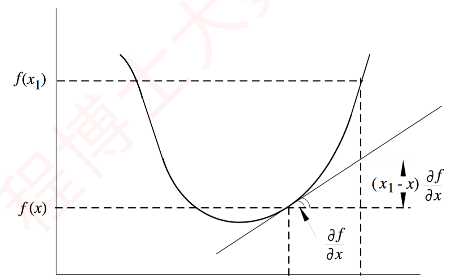
一阶充要条件：$f(x_{1}) \ge f(x)+\triangledown^{T}f(x)(x_{1}-x)$对于所有$x_{1},x$均成立，参考下图；
二阶充要条件：如果函数$f$二阶可导，则凸函数的充要条件是：$H(x) \succeq 0$；

凸优化问题标准形式

凸优化问题标准形式可以表示为：

$minimize \quad f_{0}(x) \\ \begin{align*} subject \ to: \ & f_{i}(x) \le 0, \quad for \ i=1,2,...,m \\ & h_{i}(x) = 0 \quad for \ i=1,2,...,p \end{align*}$

如果有：

目标函数$f_{0}=(x)$是凸的；
不等式约束函数是凸的（注意若干个凸不等式约束的交集也是凸的）；
等式约束是仿射的；
那么凸优化问题就是在一个凸集上极小化一个凸的目标函数；此时的最优值（目标函数在可行域上的最小值）可以表示为： $f_{0}(x^{*})=p^{*}$ 其中， $p^{*}=\min{\{f_{0}(x):f_{i}(x) \le 0,h_{i}(x)=0\}}$

凸优化问题的重要结论

凸优化问题局部最优就是全局最优，特别得，对于无约束优化来说，即代表梯度等于0，迭代法始终会收敛域最优值。

典型的凸优化问题

二次规划问题（QP问题）

如果$P$是半正定的（则目标函数是凸的，这点博主也未能深究下去），二次规划问题可以表示为：

$minimize \quad \frac{1}{2}x^{T}Px+c^{T}x+d \\ \begin{align*} subject \ to: \ & Gx \le h \\ & Ax = b \end{align*}$

其中大写字母表示矩阵，公式可以表述为，如果目标函数是凸的二次型，不等式约束条件是凸的，等式约束是仿射的，那么就是一个凸优化问题。

SVM预热

ok，以上讨论的问题如果有不懂的其实不必深究，博主也一样，我们且当作结论来看待。下面看下图形式的一个问题：

实际上，上面这个问题就是SVM的优化问题，具体是怎么得来的我们在后续的博文中将介绍。我们现在考虑如何将上述问题转化成一个QP问题，就相当于转化成了一般凸优化问题。
对照上图目标函数，和QP问题的目标函数，我们可以假设值

$x \in R^{k} = [w \ \xi \ b]^{T}, \ X \in R^{m \times n}=[x_{1}^{T},...,x_{m}^{T}]^{T}, y \in R{m}=[y_{1}, ... , y_{m}]^{T}$

实际问题中，m可以理解为数据量，n或k可以暂时理解为维度。然后我们对应目标式和QP问题构造$P,c,G,h$如下图，其中$diag$表示构造为对角矩阵。

手敲Latex有点懵逼，偷下懒在纸上手动推了一下SVM目标函数对应QP问题目标函数的过程：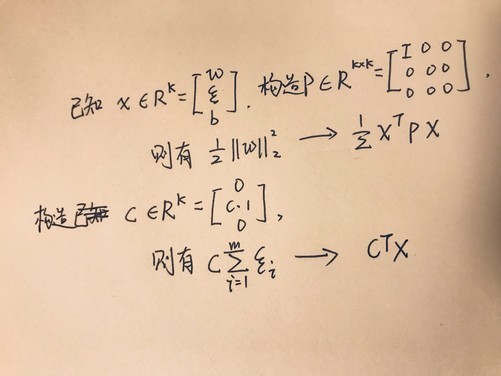

约束函数的对应构造也是如此。

总结

这里主要是阐述了凸优化问题的基本概念和典型形式，同时通过了简单的推导解释了如何将SVM的优化问题转化为QP问题。