本文是SVM三部曲第二部分—凸优化对偶。对偶是一个神奇的方法，对于一般有约束优化问题，如果难以求得最优解，那么可以尝试使用对偶方法。

本文是SVM三部曲中的第二篇。知识点和文章结构是学习了稀牛学院数学基石课程后的总结。
SVM三部曲之凸优化问题
 SVM三部曲之凸优化对偶
 SVM三部曲之SVM终极推导

对偶方法是一种可以很方便求解凸优化问题的方法。对于一般优化问题如下：

$minimize \quad f_{0}(x),x \in S \\ \begin{align*} subject \ to: \ & f_{i}(x) \le 0, \quad for \ i=1,2,...,m \\ & h_{j}(x) = 0 \quad for \ j=1,2,...,p \end{align*}$

其中可行域为 $f_{i}$ 和 $h_{j}$ 的可行域的交集。

原问题转换

优化问题可以使用拉格朗日函数来表示。接下来，我们通过构造拉格朗日函数将目标函数和约束合并：

$L(x,\lambda,v)=f_{0}(x)+\sum_{i=1}^{m}\lambda_{i}f_{i}(x)+\sum_{j=1}^{p}v_{j}h_{j}(x)$

其中，主变量为 $x$，对偶变量 $\lambda \ge 0, v$

那么原始问题可以写为（原因后面我们解释）：

$p^{*}=\min_{x} \big(\max_{\lambda,v} L(x,\lambda,v) \big)$

其中，$p^{*}$ 在第一部分中提到，是原问题的最优点取值。我们先看 $max$ 部分，由于是对对偶变量的域求最大，那么 $max$ 部分可以写为：

$\max_{\lambda,v}L(x,\lambda,v)=f_{0}(x)+\max_{\lambda,v}\big(\sum_{i=1}^{m}\lambda_{i}f_{i}(x)+\sum_{j=1}^{p}v_{j}h_{j}(x)\big)$

实际上就变成了对后面两项求最大。如果$x$在可行域内即 $x \in D$，那么不等式约束 $f_{i}(x) \le 0$，等式约束 $h_{j}(x)=0$，所以有后面一项最大能取到0，于是如果 $x$ 在可行域内，有：

$\max_{\lambda,v}L(x,\lambda,v)=f_{0}(x)$

如果 $x$ 不在可行域内，那么 $max$ 项为无穷。于是主问题就可以直观理解为，在可行域内寻找目标函数的极小值。我们一般的优化问题便得到了转换，接下来就基于转换后的主问题展开。这使得拉格朗日对偶函数与主问题完美融合，也就解释了刚刚为什么主问题这样写的原因。

对偶问题

接下来，是一个很关键的步骤，就是 $max$ 和 $min$ “位置互换”，也就是变成

$d^{*}=\max_{\lambda,v} \big( \min_{x}L(x,\lambda,v)\big)$

那么就得到了对偶函数：

$g(\lambda,v)=\min_{x \in S}L(x,\lambda,v)=\min_{x \in S}\big\{ f_0(x)+\sum_{i=1}^{m}\lambda_{i}f_{i}(x)+\sum_{i=1}^{p}v_{j}h_{j}(x) \big\}=\min_{x \in S}\big\{ f_0(x)+\lambda^{T}F+v^{T}H \big\}$

注意到对偶空间后，$x$ 可以取到定义域的值，如果给定一个 $x$ 的情况下，$g(\lambda,v)$ 实际上是一个关于 $\lambda和v$ 的仿射函数，而仿射函数是即凸且凹的（这是结论）。在 $min$ 的情况下，变成了对仿射函数求逐点下界，总是凹的，这使得原问题非凸，因为不管原问题是否是凸问题，$f_{0}(x)$ 在拉格朗日对偶函数实际就是一个常数而已。那么我们就能对对偶函数求一个最大值。
接下来，我们假设 $\tilde{x}$ 是 $x$ 可行域中的一个值，那么有：

$g(\lambda,v)=\min_{x \in S}L(x,\lambda,v) \le L(\tilde{x},\lambda,v)$

同时，因为 $\lambda和v$ 的取值限制，有：

$L(\tilde{x},\lambda,v)=f_{0}(\tilde{x})+\sum_{i=1}^{m}\lambda_{i}f_{i}(\tilde{x})+\sum_{j=1}^{p}v_{j}h_{j}(\tilde{x}) \le f_{0}(\tilde{x})$

所以，当$x$取到原问题的最优点即 $x=x^{*}$ 时，也有：

$g(\lambda,v) \le f_{0}(x^{*})=p^{*}$

ok，现在我们知道了对偶函数始终是小于原问题最优点的，那么我们为何不尝试去寻找对偶函数的最大值去逼近原问题的最优点呢？。就像下图：

于是对偶问题可以描述为：

$maximize \ \ g(\lambda,v) \\ subject \ to: \ \lambda \ge 0$

可以理解为凹函数在凸集上的最大化，这本质上也是一个凸优化问题（凹凸形状是映射的），这里我们发现，我们一开始的假设是一般的优化问题，那么原问题 $\min{f_{0}(x)}$ 即使不是凸优化问题，但是转换成对偶问题后，这就变成了一个凸优化问题。我们假设最优值为 $d^{*}$ ($d^{*} \le p^{*}$)，对应的极值点为 $\lambda^{*},v^{*}$。

对偶的几何解释

接下来以下图为例，我们将对偶放在几何空间上进行解释。

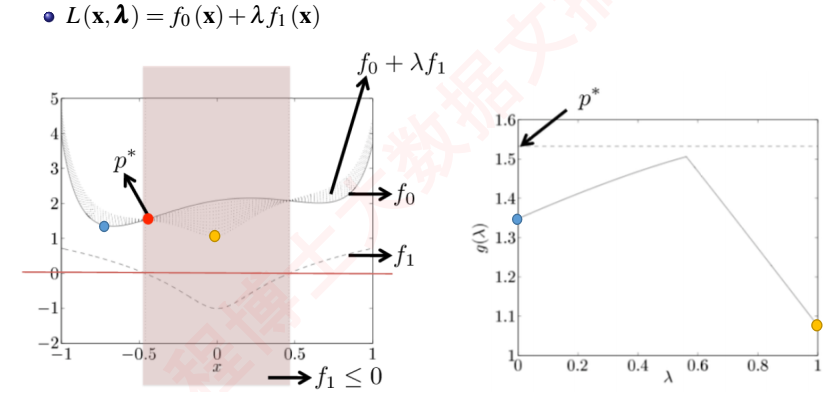
假设我们构建了一个拉格朗日函数，左图是原问题坐标系，右图是对偶问题坐标系，我们先看左图：

$L(x,\lambda)=f_{0}(x)+\lambda f_{1}(x)$，函数对应的曲线如图中标注；
约束是 $f_{1} \le 0$，那么对应到原问题中 $x$ 的可行域就是图中粉色的部分， $-0.48 \le x \le 0.48$ 左右；灰色区域的边缘曲线对应为 $L$
我们可以清楚得看到，在可行域中，最小值对应于 $x=-0.48$，即图中 $p^{*}$ ；
根据我们的限制， $\lambda \ge 0$，当 $\lambda=0$ 时，$L$ 的曲线即为 $f_{0}$ 的曲线，此时对偶函数 $g$ 的取值为蓝点（为什么能取到蓝点？因为粉色区域是原问题的可行域，到对偶问题后，可以取 $x$ 的定义域），参考右图坐标中的蓝点；当 $\lambda=1$ 时，$L$ 的曲线为图中灰色区域的边缘曲线，此时对偶函数 $g$ 的取值为黄点，参考右图坐标中的黄点；我们可以发现此时只有在 $\lambda=0.55$ 附近时，对偶函数 $g$ 对应的最大值 $d^{*}$ 才是最接近原问题最小值 $p^{*}$。

强弱对偶解释

弱对偶： $d^{*} \le p^{*}$，无论凸或非凸问题总成立；
强对偶： $d^{*} = p^{*}$；此条件通常不成立，对于凸优化问题通常成立；同时需要满足Slater条件：存在内点 $x$，使得 $f_{i}(x) < 0 \ \ for \ i=1,2,…,m$ 均成立，即存在一个点是得每个不等式约束都小于0。这个我们当作结论看就ok。

从对偶问题解主问题

假设强对偶成立， $(x^{*},\lambda^{*},v^{*})$ 是主对最优解，有：

$\begin{align*} p^{*}=f_0(x^{*}) &= d^{*}=g(\lambda^{*},v^{*}) \\ &=\min_x\big(f_0(x)+\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}(x)+\sum_{j=1}^{p}v_{j}^{*}h_{j}(x)\big) \\ &\le f_0(x^{*})+\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}(x^{*})+\sum_{j=1}^{p}v_{j}^{*}h_{j}(x^{*}) \\ &\le f_0(x^{*}) \end{align*}$

上面的式子不难理解，实际上就是前面叙述中的总结。第三行和第四行的式子中，由于条件 $\lambda \ge 0, \ f_i(x^{*}) \le 0, h_j(x^{*})=0$，故小于等于 $f_0(x^{*})$。那么我们可以发现式中得到的一个重要结果是： $f_0(x^{*}) \le f_0(x^{*})$ ！因此上式中所有的小于等于号实际上就是等号，同时意味着 $\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}(x)=0$，可以改写为：

$\begin{align*} p^{*}=f_0(x^{*}) &= d^{*}=g(\lambda^{*},v^{*}) \\ &=\min_x\big(f_0(x)+\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}(x)+\sum_{j=1}^{p}v_{j}^{*}h_{j}(x)\big) \\ &= f_0(x^{*})+\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}(x^{*})+\sum_{j=1}^{p}v_{j}^{*}h_{j}(x^{*}) \\ &= f_0(x^{*}) \end{align*}$

于是，根据新的式子，我们可以得到以下结论：

结论一： $\lambda^{*}f_i(x^{*})=0$；
结论二： $g(\lambda^{*},v^{*})=L(x^{*},\lambda^{*},v^{*})=\min_xL(x,\lambda^{*},v^{*})$，这相当于拉格朗日函数在给定 $\lambda^{*},v^{*}$ 下对 $x$ 求最小值，也就意味着对 $x$ 求梯度 $\triangledown_xL(x^{*},\lambda^{*},v^{*})=0$；

博主认为这是非常恶心且精彩的结论，每一步都是由前面的铺垫而得到的。

KKT条件

ok，我们重新回顾整理一下，假设有一个凸优化问题：

$minimize \quad f_{0}(x),x \in S \\ \begin{align*} subject \ to: \ & f_{i}(x) \le 0, \quad for \ i=1,2,...,m \\ & h_{j}(x) = 0 \quad for \ j=1,2,...,p \end{align*}$

我们对其构造一个拉格朗日函数：

$L(x,\lambda,v)=f_{0}(x)+\sum_{i=1}^{m}\lambda_{i}f_{i}(x)+\sum_{j=1}^{p}v_{j}h_{j}(x)$

假设 $x^{*}$ 是原问题最优解取值，$(\lambda^{*},v^{*})$ 是对偶问题最优解取值。如果凸优化问题的强对偶条件成立，那么其充要条件是：

$f_i(x^{*}) \le 0 \ \ i=1,…,m$
$h_j(x^{*}) = 0 \ \ j=1,…,p$
$\lambda^{*} \ge 0 \ \ i=1,…,m$
$\sum_{i=1}^{m}\lambda_{i}^{*}f_{i}(x^{*})=0$
$\triangledown_xL(x,\lambda^{*},v^{*})=\triangledown f_0(x)+\sum_{i=1}^{m}\lambda_{i}^{*} \triangledown f_{i}(x)+\sum_{j=1}^{p}v_{j}^{*} \triangledown h_{j}(x)=0$

以上五个条件称为KKT条件。

主对（对偶）问题回顾

主问题是：

$p^{*}=\min_x \big( \max_{\lambda \ge 0, v} L(x,\lambda,v)\big)$

对偶问题是：

$d^{*}=\max_{\lambda \ge 0, v} \big( \min_x L(x,\lambda,v)\big) \big)$

强对偶成立时，$max$ 和 $min$ 互换：

$\max_{\lambda \ge 0, v} \big( \min_x L(x,\lambda,v)\big) \big) = \min_x \big( \max_{\lambda \ge 0, v} L(x,\lambda,v)\big)$

举个栗子

假设我们求解下列问题，这个问题满足强对偶条件：

$minimize \ {\Arrowvert x \Arrowvert}_2^2 \\ s.t. \ Ax=b$

构造拉格朗日函数：

$L(x,v)=x^Tx+v^T(Ax-b)$

对偶函数：

$g(v)=\min_xL(x,v)$

$g$ 对 $x$ 求极值，另其梯度为0，即：

$\triangledown_xL(x,v)=0 \Rightarrow 2x+A^Tv=0 \Rightarrow x^{*}(v)=-\frac{1}{2}A^Tv$

将 $x^{*}$ 代入到对偶函数中：

$g(v)=L(x^{*},v)=-\frac{1}{4}v^T(AA^T)v-v^Tb$

$g(v)$ 是一个凹函数，为什么？除去 $\frac{1}{4}$ 前的负号，这是一个QP（二次规划）问题，那么加上这个负号，就变成了凹函数，那么它就存在一个最大值：

$d^{*}=\max_v -\frac{1}{4}v^T(AA^T)v-v^Tb$

还记得我们前面说的强对偶的结论吗？既然它是一个凹函数，我们就对 $v$ 通过梯度等于0求它最大值点：

$v^{*}=-2(AA^T)^{-1}b \\ d^{*}=b^T(AA^T)^{-1}b$

将 $v^{*}$ 带入 $x^{*}(v)$ 得：

$x^{*}=A^T(AA^T)^{-1}b$

总结

其实这一部分将的内容可以总结为，通过对偶问题来求解原始问题。我们首先将原始问题用拉格朗日函数表示，然后将 $max$ 和 $min$ 进行对换，得到对偶问题。如果满足强对偶条件，我们就可以根据KKT条件，由拉格朗日函数对 $x$ 求梯度为0，得到对 $x$ 关于对偶变量的最优解。将结果代回对偶函数中，发现对偶函数是凹函数，于是再对对偶函数求最大值，由于强对偶，得到的结果就和原问题的最小值一致。
以上是我对凸优化对偶的一些总结，敲公式敲得有点累，但是可以加深理解。