本文是SVM三部曲最后一部分—SVM终极推导。讲解了SVM的思想，目标方程的简化以及使用对偶方法进行求解。

本文是SVM三部曲中的最后一篇。知识点和文章结构是学习了稀牛学院数学基石课程后的总结。
SVM三部曲之凸优化问题
 SVM三部曲之凸优化对偶
 SVM三部曲之SVM终极推导

线性分类器和最优线性分类器

假设一个线性可分的二分类情况，我们总能在空间中找到一个边界 $w^{T}x+b=0$ 来切分。最简单的方法就是感知机算法，相关可以参考博文感知机算法。事实上，这样的超平面有无数多个，那么，哪一个是最优的呢？SVM了解一下。

点到超平面的距离

假设有超平面：

$H=\{w^{T}x+b=0\}$

那么空间中任意一点 $p$ 到平面的距离可以表示为：

$r = \frac{\mid w^{T}p+b \mid}{ \parallel w \parallel_{2}}$

这个大家应该都比较熟悉吧，博主记得高中的时候好像就学过这个公式。这里我们来推导一下吧，请忽略我规（潦）整（草）的字体：

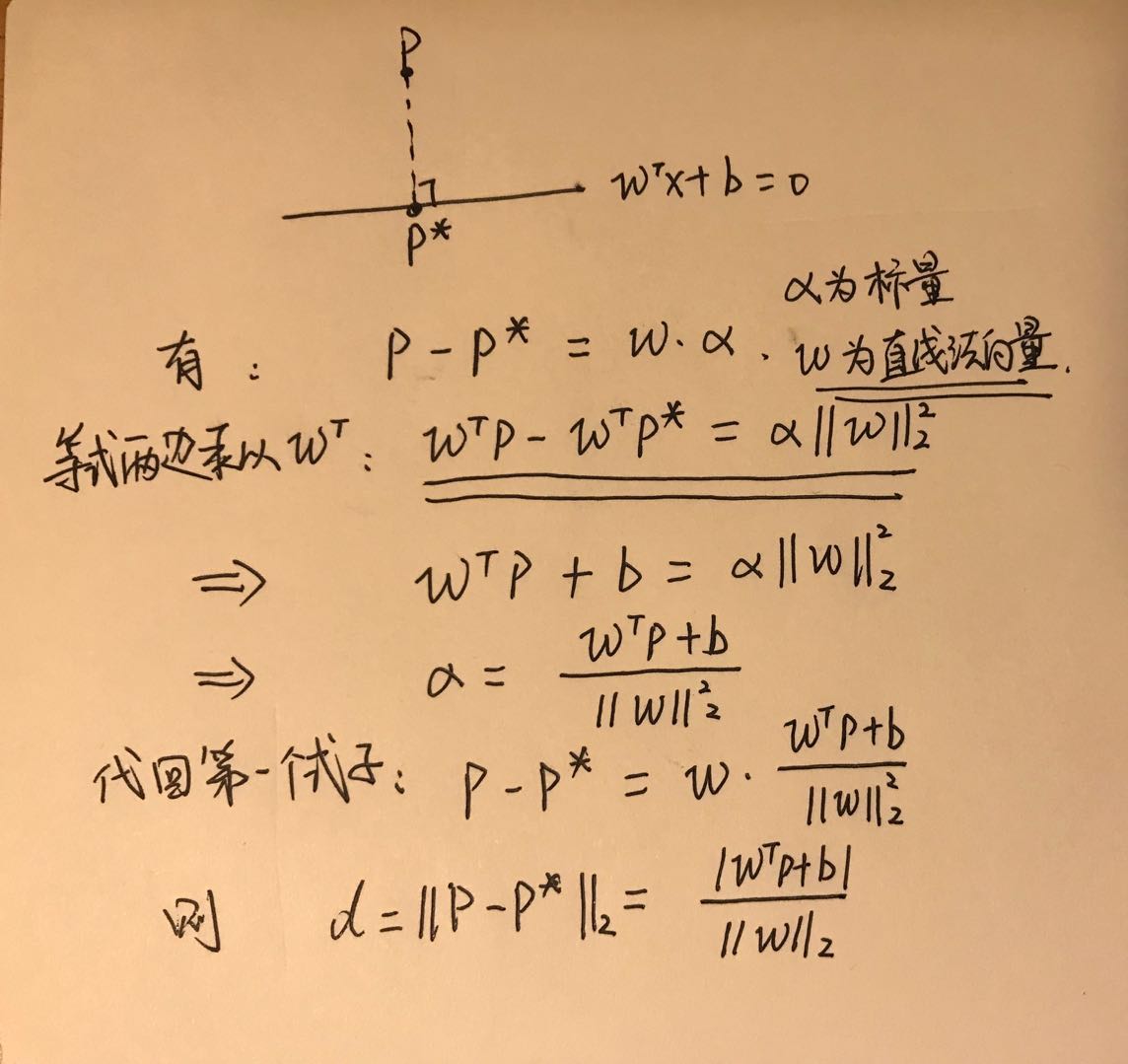
求解的方式有很多，可以百度参考解法汇总：https://www.zhihu.com/question/37199042

SVM目标函数

点集到分类面的最小距离可以表示为：

$M=\min_{i} r_{i} = \min_{i} \frac{\mid w^{T}x_{i}+b \mid}{ \parallel w \parallel_{2}}$

我们把点集到分类面最小的距离称之为几何间隔，也就是 margin。接下来我们引出SVM的目标函数：

$\max_{w,b} M = \max_{w,b} \Big\{ \min_{i} \frac{\mid w^{T}x_{i}+b \mid}{ \parallel w \parallel_{2}} \Big\}$

也就是 间隔最大化 。试想，如果我们让最接近分类面的样本点的距离最大化，不就可以尽可能把样本点都分开了么？就是这么简单暴力的思想。

然而，对于这样一个明确的优化问题，直接求解是十分困难的。接下来，我们尝试简化一下目标函数。

简化目标函数

首先，我们从绝对值项入手，将 $\mid w^{T}x_{i}+b \mid$ 项改写为：

$y_{i}(w^{T}x_{i}+b)$

这转换大家体会一下是不是这样的？和感知机算法的小技巧神似，于是目标函数相应变为：

$\max_{w,b} M = \max_{w,b} \Big\{ \frac{1}{\parallel w \parallel_{2}} \min_{i} y_{i}(w^{T}x_{i}+b) \Big\}$

接下来，使用另一个小技巧。我们试想一下，一条直线的 $w$ 和 $b$ 如果同时乘上一个系数 $k$ 后，仍然是等同的，即 $w^{T}+b=0$ 与 $kw^{T}+kb=0$ 是等同的。应用到目标函数后，将 $w$ 和 $b$ 如果同时乘上一个系数 $k$ ，进行一个scale，其距离并不发生变化：

$\frac{\mid kw^{T}x+kb \mid}{ \parallel kw \parallel_{2}}=\frac{\mid w^{T}x+b \mid}{ \parallel w \parallel_{2}}$

因此，通过修改 $k$，我们可以设计距离最近的一个点，使得：

$y_{i}(w^{*T}x_{i}+b^{*})=1$

其中 $w^{*}=kw,\ b^{*}=kb$ 。
既然最近的点满足 $y_{i}(w^{*T}x_{i}+b^{*})=1$ ，那么所有的点能满足下式：

$y_{i}(w^{*T}x_{i}+b^{*}) \ge 1, \ i=1,...,N$

ok，我们再回过头看一下目标函数，里面的 $\min_{i} y_{i}(w^{T}x_{i}+b)$ 是不是就等于 1 了嗯？ $\min$ 这项就这样被我们干掉了，牛逼的地方来了。
最后，我们把 $\frac{1}{\parallel w \parallel_{2}}$ 倒过来再加上平方（为什么要平方，因为 $\parallel w \parallel_{2}$ 是有开根号的，而我们在优化的时候通常不喜欢这个东西，所以干脆加个平方，加之前是最小化一个正数，加之后也是最小化一个正数，没毛病），那么目标优化问题就最终简化完成，SVM基本型：

$\min \frac{1}{2} \parallel w \parallel_{2}^{2} \\ s.t. \ y_{i}(w^{T}x_{i}+b) -1 \ge 0, \ i=1,...,N$

我们来看一下几何解释：

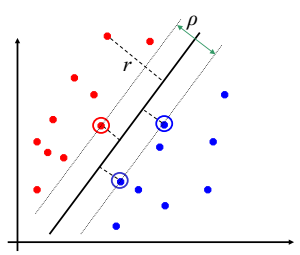
图中的分界线为 $w^{T}x+b=0$ ,根据我们的scale后，图中穿过距离分界线最近的红点的平行线可以认为是 $w^{T}x+b=1$，穿过距离分界线最近的蓝点的平行线可以认为是 $w^{T}x+b=-1$，原因是在scale后，有 $y_{i}(w^{*T}x_{i}+b^{*})=1$ 。图中的里分界线最近的一个红点和两个蓝点就被我们称为支撑向量。而支撑向量到分界线的距离是：

$margin=\frac{\mid w^{T}x+b \mid}{ \parallel w \parallel_{2}}=\frac{1}{ \parallel w \parallel_{2}}$

我们希望margin最大，也就是希望margin的倒数的平方 $\parallel w \parallel_{2}^{2}$ 最小，这样和目标函数统一了。

SVM求解

上面说到，经过我们的简化，SVM的目标函数变成了：

$\min \frac{1}{2} \parallel w \parallel_{2}^{2} \\ s.t. 1 - \ y_{i}(w^{T}x_{i}+b) \le 0, \ i=1,...,N$

是不是感觉很眼熟，我们在《SVM三部曲之凸优化问题》结尾中提到过类似的问题。这实际上是一个QP二次规划问题，QP问题还有印象不？ $\frac{1}{2} \parallel w \parallel_{2}^{2}$ 我们可以写成形式 $\frac{1}{2} w^{T}Iw$，而 $I$ 是一个正定矩阵，同时不等式约束是凸的，于是我们的目标就变成了一个凸优化问题。

SVM对偶问题

ok，我们已经知道SVM的目标问题是一个凸优化问题了，显然约束条件也满足 slater 条件，那么SVM问题强对偶成立，同时 KKT 条件成立。于是我们可以将主问题转换成对偶问题来求解。
构建拉格朗日函数：

$L(w,b,\lambda)=\frac{1}{2} \parallel w \parallel_{2}^{2} + \sum_{i=1}^{N} \lambda_{i}(1-y_{i}(w^{T}x_{i}+b)) \\ \lambda_{i} \ge 0,\ i=1,...,N$

主问题是：

$p^{*}=\min_{w,b} \big(\max_{\lambda}L(w,b,\lambda)\big)$

对偶问题是：

$d^{*}=\max_{\lambda} \big(\min_{w,b}L(w,b,\lambda)\big) \\ g(\lambda)=\min_{w,b}L(w,b,\lambda)$

对于 $\min$ 部分，我们对 $w,b$ 分别求偏导并令其为 $0$，并求得：

$w=\sum_{i=1}^{N}\lambda_{i}y_{i}x_{i}, \quad 0=\sum_{i=1}^{N}\lambda_{i}y_{i}$

将结果代入对偶问题中有：

$\begin{align*} \max_{\lambda}g(\lambda) &= \max_{\lambda}\big( \frac{1}{2} \parallel w \parallel_{2}^{2} + \sum_{i=1}^{N} \lambda_{i}(1-y_{i}(w^{T}x_{i}+b))\big) \\ &=\max_{\lambda}\big( -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum_{i=1}^{N}\lambda_{i} - \sum_{i=1}^{N}\lambda_{i}y_{i}(w^{T}x_{i}+b) \big) \\ &=\max_{\lambda}\big(-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j} + \sum_{i=1}^{N}\lambda_{i}\big) \end{align*} \\ s.t. \ \sum_{i=1}^{N}\lambda_{i}y_{i}=0, \ \lambda_{i} \ge 0, \ i=1,...,N$

因为SVM是满足强对偶，我们能够解出最优解 $\lambda^{*}$，根据 KKT 充要条件有：

$1-y_{i}(w^{*T}x_{i}+b^{*}) \le 0$
$\lambda_{i}^{*} \ge 0$
$\lambda_{i}^{*}(1-y_{i}(w^{*T}x_{i}+b^{*}))=0 $
$w^{*}=\sum_{i=1}^{N}\lambda^{*}_{i}y_{i}x_{i}, \quad 0=\sum_{i=1}^{N}\lambda^{*}_{i}y_{i}$

到这里，我们就解出了参数 $w^{*}$ ，我们看一下 KTT 结论带来的一些理解：

如果 $\lambda^{*}_{j}=0$，就相当于对 $w^{*}$ 毫无贡献；
如果 $\lambda^{*}_{j}>0$，则 $y_{i}(w^{*T}x_{i}+b^{*}=1$，为支撑向量；
此时，将 $w^{*}$ 带入到 $y_{i}(w^{*T}x_{i}+b^{*}=1$，可以解出 $b^{*}=y_{j}-(\sum_{i=1}^{N}\lambda^{*}y_{i})(x^{T}_{i}x_{j})$

此时 $\lambda^{*}$ 是一个稀疏的解，大于零的对应支撑向量，等于零的对应非支撑向量。

SVM最终步骤

上面说到，如果我们解出了 $\lambda^{}$，我们就能解出 $w^{},b^{*}$。那么最优的分类超平面为：

$w^{*T}x+b^{*}=0 \\ \sum_{i=1}^{N}\lambda^{*}y_{i}x_{i}x+b^{*}=0$

决策函数就为：

$f(x)=sign\big(\sum_{i=1}^{N}\lambda^{*}y_{i}x_{i}x+b^{*}\big)$

可以看到，最终的分类超平面仅由 $\lambda^{*}>0$，也就是支撑向量起到了作用。

SMO求解 $\lambda^{*}$

求解下列无约束优化问题：

$\max_{\lambda}W(\lambda_{1},...,\lambda_{m})$

可以使用SMO算法求解到 $\lambda^{*}$，这里博主没有深入研究下去了，感兴趣的同学可以了解一下啦。

SVM软间隔

上面讨论的是数据线性可分的情况，但是实际中，往往会有噪声点使得数据集并不是线性可分的。这是SVM目标函数可以加上一个惩罚项：

$\min \frac{1}{2} \parallel w \parallel_{2}^{2}+C\sum_{i=1}^{N}\xi_{i} \\ s.t. \ y_{i}(w^{T}x_{i}+b) \ge 1-\xi_{i}, \ i=1,...,N; \ \xi_{i} \ge 0$

后续到对偶问题过程中，也对 $\xi$ 求偏导为0，然后同样带入 $g(\lambda)$ 进行求解。

kernel核函数

关于核函数，其实和SVM是两个领域，比较直观的理解可以参考知乎上的这条帖子：https://www.zhihu.com/question/24627666
当数据线性不可分的时候，我们可以借助核函数将原输入空间映射到线性可分的空间来。对于核函数，博主会找个时间另外开个博文来进行学习。