ResNet残差神经网络是何凯明博士于2016年提出的，其相关论文获得了当年CVPR的best parer。计算机视觉领域中，可以证明更深的神经网络可以学习更好的特征，取得更好的识别成绩。虽然ReLU、dropout等方法减小了深层神经网络训练过程中梯度弥散的影响，训练深层的网络依然会出现退化(degradation)的情况。而ResNet的提出，使得更深层的网络得以训练。
以下内容为学习论文和参考其他资料后的简单总结，包含实现代码。

ResNet

原理

计算机视觉领域中，更深层次的神经网络可以学习到更深的特征。VGG和GoogleNet分别依靠19层、22层的网络结构在ILSVRC2014比赛中将错误率降低到了7.3、6.7。
所以，学习更好的网络是否与堆叠更多层数一样简单呢？

Is learning better networks as easy as stacking more layers?

答案是否，梯度弥散/爆炸问题依然阻碍收敛的最大障碍。虽然ReLU、dropout等方法可以缓解这个情况。当一个更深的网络开始收敛时，会出现一个称为退化（原文为degradation）的现象：深度增加，准确率开始饱和后开始迅速衰减。退化现象并不是由于过拟合所导致的，对现有性能不错的网络增加层数后获得了更高的错误率。下图中可以看到，目前的平原网络结构（论文称为“plain”）下，56层的网络与20层的网络相比，无论是在训练集上还是测试集上，其错误率都要更高。这是一个在许多数据集中都能观察到的普遍现象。

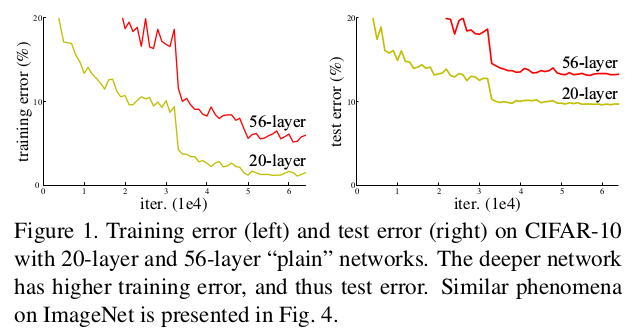
为此，论文有了这样一个想法：将增加的层作为恒等映射。deep residual learning 框架应运而生。

Let us consider a shallower architecture and its deeper counterpart that adds more layers onto it. There exists a solution by constructionto the deeper model: the added layers are identity mapping, and the other layers are copied from the learned shallower model.

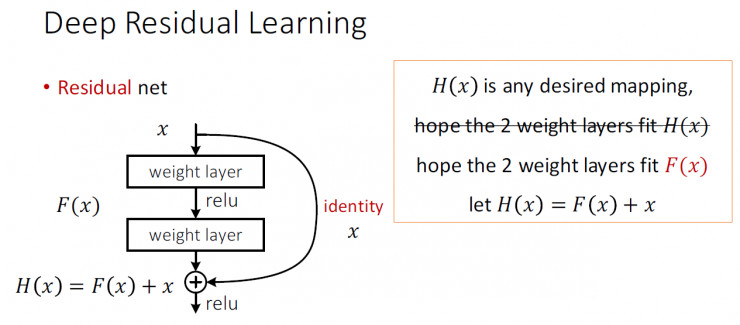
如下图平原网络中，$H(x)$是期望的映射，我们希望学习到拟合$H(x)$的两层网络参数。

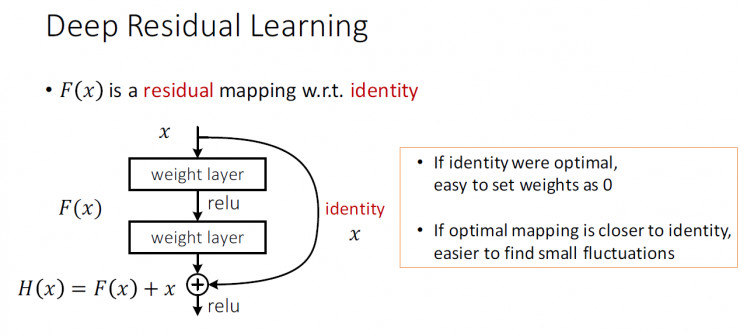
残差网络中，把$H(x)$包装一下变成下图，$H(x)=F(x)+x$，$F(x)$称为残差映射。那问题就转换为学习$F(x)$，如果$F(x)=0$，那么就是恒等映射；如果接近恒等映射，便更容易发现微小波动。
论文认为这两种表达的效果相同，但是优化的难度却并不相同，论文假设$F(x)$的优化会比$H(x)$简单的多。这一想法也是源于图像处理中的残差向量编码，通过一个reformulation，将一个问题分解成多个尺度直接的残差问题，能够很好的起到优化训练的效果。$H(x)=F(x)+x$可以用“shortcut connections”(skipping one or more layers)形式表现，如下图中左边的网络结构.

论文就上述观点做了相关实验，具体可以参考论文resnet
大神的一点思维波动，作为学渣的我就得好生理解一番。看了论文后，实际上还是很难直观搞清楚：为什么这样就会解决退化的问题？why给了一个合理的解释，如果你熟悉反向传播的链式原理，就很容易理解。

实战

import torch
import torch.nn as nn
import torchvision.datasets as dsets
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
from torch.autograd import Variable
from torch.utils.data import DataLoader

加载训练集图片的预处理日常操作

transform = transforms.Compose([
    transforms.Resize(40),
    transforms.RandomHorizontalFlip(),
    transforms.RandomCrop(32),
    transforms.ToTensor()
])

如果没有下载数据集，设置download参数为True

train_dataset = dsets.CIFAR10(root='./data/',
                               train=True, 
                               transform=transform,
                               download=False)

test_dataset = dsets.CIFAR10(root='./data/',
                              train=False, 
                              transform=transforms.ToTensor())

train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
                                           batch_size=100, 
                                           shuffle=True)

test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
                                          batch_size=100, 
                                          shuffle=False)

3x3卷积

1
2
3

def conv3x3(in_channels, out_channels, stride=1):
    return nn.Conv2d(in_channels, out_channels, kernel_size=3, 
                     stride=stride, padding=1, bias=False)

定义残差单元 ResidualBlock

class ResidualBlock(nn.Module):
    def __init__(self, in_channels, out_channels, stride=1, downsample=None):
        super(ResidualBlock, self).__init__()
        self.conv1 = conv3x3(in_channels, out_channels, stride)
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(out_channels, out_channels)
        self.bn2 = nn.BatchNorm2d(out_channels)
        self.downsample = downsample
        
    def forward(self, x):
        residual = x
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        out = self.conv2(out)
        out = self.bn2(out)
        if self.downsample:
            residual = self.downsample(x)
        out += residual
        out = self.relu(out)
        return out

class ResNet(nn.Module):
    def __init__(self, block, layers, num_classes=10):
        super(ResNet, self).__init__()
        self.in_channels = 16
        self.conv = conv3x3(3, 16)
        self.bn = nn.BatchNorm2d(16)
        self.relu = nn.ReLU(inplace=True)
        self.layer1 = self.make_layer(block, 16, layers[0])
        self.layer2 = self.make_layer(block, 32, layers[0], 2)
        self.layer3 = self.make_layer(block, 64, layers[1], 2)
        self.avg_pool = nn.AvgPool2d(8)
        self.fc = nn.Linear(64, num_classes)
        
    def make_layer(self, block, out_channels, blocks, stride=1):
        downsample = None
        if (stride != 1) or (self.in_channels != out_channels):
            downsample = nn.Sequential(
                conv3x3(self.in_channels, out_channels, stride=stride),
                nn.BatchNorm2d(out_channels))
        layers = []
        layers.append(block(self.in_channels, out_channels, stride, downsample))
        self.in_channels = out_channels
        for i in range(1, blocks):
            layers.append(block(out_channels, out_channels))
        return nn.Sequential(*layers)
    
    def forward(self, x):
        out = self.conv(x)
        out = self.bn(out)
        out = self.relu(out)
        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.avg_pool(out)
        out = out.view(out.size(0), -1)
        out = self.fc(out)
        return out

1 2	resnet = ResNet(ResidualBlock, [3, 3, 3]) resnet.cuda()

ResNet(
  (conv): Conv2d (3, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
  (bn): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True)
  (relu): ReLU(inplace)
  (layer1): Sequential(
    (0): ResidualBlock(
      (conv1): Conv2d (16, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (16, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True)
    )
    (1): ResidualBlock(
      (conv1): Conv2d (16, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (16, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True)
    )
    (2): ResidualBlock(
      (conv1): Conv2d (16, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (16, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True)
    )
  )
  (layer2): Sequential(
    (0): ResidualBlock(
      (conv1): Conv2d (16, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True)
      (downsample): Sequential(
        (0): Conv2d (16, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (1): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True)
      )
    )
    (1): ResidualBlock(
      (conv1): Conv2d (32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True)
    )
    (2): ResidualBlock(
      (conv1): Conv2d (32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True)
    )
  )
  (layer3): Sequential(
    (0): ResidualBlock(
      (conv1): Conv2d (32, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True)
      (downsample): Sequential(
        (0): Conv2d (32, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True)
      )
    )
    (1): ResidualBlock(
      (conv1): Conv2d (64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True)
    )
    (2): ResidualBlock(
      (conv1): Conv2d (64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True)
      (relu): ReLU(inplace)
      (conv2): Conv2d (64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True)
    )
  )
  (avg_pool): AvgPool2d(kernel_size=8, stride=8, padding=0, ceil_mode=False, count_include_pad=True)
  (fc): Linear(in_features=64, out_features=10)
)

1
2
3

criterion = nn.CrossEntropyLoss()
lr = 0.001
optimizer = torch.optim.Adam(resnet.parameters(), lr=lr)

for epoch in range(80):
    for i, (images, labels) in enumerate(train_loader):
        images = Variable(images.cuda())
        labels = Variable(labels.cuda())
        
        optimizer.zero_grad()
        outputs = resnet(images)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        
        if (i+1) % 100 == 0:
            print('epoch: {}, iter: {}, loss: {}'.format(epoch, i, loss.data[0]))
    
    if (epoch+1) % 20 == 0:
        lr /= 3
        optimizer = torch.optim.Adam(resnet.parameters(), lr=lr)

correct = 0
total = 0
for images, labels in test_loader:
    images = Variable(images.cuda())
    outputs = resnet(images)
    _, predicted = torch.max(outputs.data, 1)
    total += labels.size(0)
    correct += (predicted.cpu() == labels).sum()

print('Accuracy: %d %%' % (100 * correct / total))

ResNet认识与实战

ResNet

原理

实战

enjoy it!