IV值与WOE

发表于

  我们知道，在常用的数据科学建模套路中，对特征工程后大量的特征进行筛选常常是不可忽视的一个步骤。在金融领域的信用卡评分模型中，又常常使用IV值的大小来作为特征筛选的依据，IV值大表示该变量的预测能力强。那么IV值怎么进行计算，为什么信用卡评分建模中又偏爱使用IV值呢？我们一起来看一下。

IV是什么

  IV是英文infomation value的简称，可以翻译为信息价值。IV的作用和信息增益、基尼系数等很相似，都是用来筛选预测能力强的特征。

IV的数学计算

  下面我们从数学角度看一下IV值的怎么计算的，在此之前我们还要先了解一下什么是WOE。

WOE是什么

  WOE是英文weight of evidence的简称，可以翻译为证据权重。它是对特征变量的一种转换编码，要对一个变量进行编码，首先要将这个变量进行一个分箱操作（即离散化处理）。假设我们将特征的取值空间分成了$n$个组，对于第$i$组，WOE计算如下：

  下面以信用评分模型场景为例，上式中，$y_{T}$表示所有逾期客户数，$n_{T}$表示所有逾期客户数，$y_{i}$表示第$i$组逾期客户数，$n_{i}$表示第$i$组逾期客户数；于是，$py_{i}$表示第$i$组的逾期客户占所有逾期客户的比例，$pn_{i}$表示第$i$组的正常客户占所有正常客户的比例。从这个公式我们可以看出来，WOE实际上表示“当前分组中逾期客户占所有逾期客户的比例”与“当前分组中正常客户占所有正常客户的比例”的差异，对上式进行变化可以得到：

  于是WOE也可以理解为表示当前组中逾期客户和正常客户的比值，与全量样本中逾期客户和正常客户的比值的差异，然后根据这个差异取对数。WOE越大，这种差异就越大，那么这个分组里逾期的可能性就越大。其实这个公式展现出来的意义是很容易理解的。

IV的计算

  对于上面的第$i$组，其IV值可以计算如下：

变量总体的IV值为所有分组的IV值的和：

代码实现

  我们以乳腺癌数据集为例，乳腺癌数据集的y变量取值0,1，总共20维变量，为简化前3维，计算其IV值。主要步骤为：

  • 获取数据集，并只取前三维；
  • 大概看一下每个变量的分布情况，手动进行简单分箱；
  • 计算每个变量的IV值并通过大小来判断预测能力；
1
2
3
4
5
6
7
8
from sklearn import datasets
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
plt.rcParams['font.sans-serif'] = ['Droid Sans Fallback']
plt.rcParams['axes.unicode_minus']=False

ubuntu的matplotlib设置中文显示

1
2
import matplotlib
zhfont = matplotlib.font_manager.FontProperties(fname='/usr/share/fonts/opentype/noto/NotoSansCJK-Thin.ttc')

获取数据

1
2
3
cancer = datasets.load_breast_cancer()
x = pd.DataFrame(cancer.data).loc[:,:2]
y = pd.DataFrame(cancer.target)

特征分布与手动分箱

  看一下三个变量的分布情况。

1
2
3
4
5
6
7
8
9
10
11
fig = plt.figure(figsize=(15, 5))
ax1 = fig.add_subplot(131)
plt.title('特征0分布', fontproperties=zhfont)
ax2 = fig.add_subplot(132)
plt.title('特征1分布', fontproperties=zhfont)
ax3 = fig.add_subplot(133)
plt.title('特征2分布', fontproperties=zhfont)
sns.distplot(x[0], ax = ax1)
sns.distplot(x[1], ax = ax2)
sns.distplot(x[2], ax = ax3)
plt.show()

png

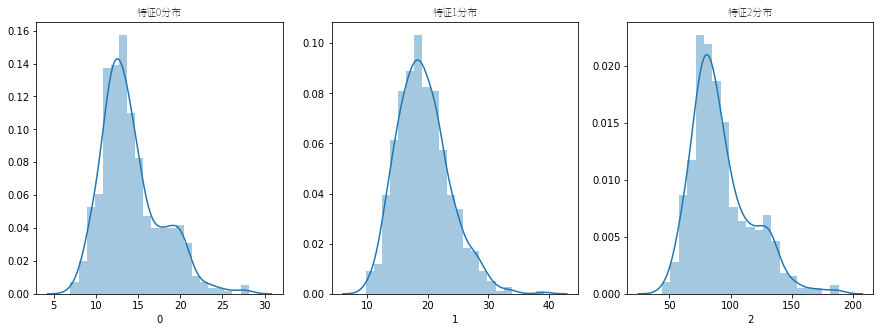
  • 特征0中，小于等于12的设置为0，大于12小于等于17的设置为1，大于17的设置为2；
  • 特征1中，小于等于16的设置为0，大于16小于等于24的设置为1，大于24的设置为2；
  • 特征2中，小于等于75的设置为0，大于75小于等于125的设置为1，大于125的设置为2；
1
2
3
4
5
6
7
def divide(x, v1, v2):
    if x <= v1:
        return 0
    elif x > v1 and x <= v2:
        return 1
    else:
        return 2
1
2
3
4
x_ = x.copy()
x_[0]=x[0].apply(divide, args=(12, 17))
x_[1]=x[1].apply(divide, args=(16, 24))
x_[2]=x[2].apply(divide, args=(75, 125))

为了模拟一下信用场景，我们可以对1样本进行一些抽样

1
2
3
4
5
6
xy = pd.concat([x_, y], axis=1)
xy.columns = ['f0', 'f1', 'f2', 'class']
xy_c1 = xy[xy['class']==1].sample(frac=0.05)
xy_c2 = xy[xy['class']==0]
xy = pd.concat([xy_c1, xy_c2], axis=0)
xy.head()
f0 f1 f2 class
378 1 0 1 1
332 0 1 0 1
46 0 1 0 1
500 1 1 1 1
463 0 1 0 1

计算WOE与IV

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 计算某组的woe
def cal_woe(py, pn):
    if pn == 0:
        return 1
    else:
        if py == 0:
            return -1
        else:
            return np.log(py / pn)

# 计算某组的iv
def cal_iv(yi, yt, ni, nt):
    py = yi / yt
    pn = ni / nt
    return (py - pn) * cal_woe(py, pn)
  • 特征0的IV值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
nt = xy[xy['class']==0].shape[0]
yt = xy[xy['class']==1].shape[0]

yi = xy[(xy['f0']==0) & (xy['class']==1)].shape[0]
ni = xy[(xy['f0']==0) & (xy['class']==0)].shape[0]
iv0 = cal_iv(yi, yt, ni, nt)

yi = xy[(xy['f0']==1) & (xy['class']==1)].shape[0]
ni = xy[(xy['f0']==1) & (xy['class']==0)].shape[0]
iv1 = cal_iv(yi, yt, ni, nt)

yi = xy[(xy['f0']==2) & (xy['class']==1)].shape[0]
ni = xy[(xy['f0']==2) & (xy['class']==0)].shape[0]
iv2 = cal_iv(yi, yt, ni, nt)

f0_iv = iv0 + iv1 + iv2
f0_iv
1.9204698528436794
  • 特征1的IV值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
yi = xy[(xy['f1']==0) & (xy['class']==1)].shape[0]
ni = xy[(xy['f1']==0) & (xy['class']==0)].shape[0]
iv0 = cal_iv(yi, yt, ni, nt)

yi = xy[(xy['f1']==1) & (xy['class']==1)].shape[0]
ni = xy[(xy['f1']==1) & (xy['class']==0)].shape[0]
iv1 = cal_iv(yi, yt, ni, nt)

yi = xy[(xy['f1']==2) & (xy['class']==1)].shape[0]
ni = xy[(xy['f1']==2) & (xy['class']==0)].shape[0]
iv2 = cal_iv(yi, yt, ni, nt)

f1_iv = iv0 + iv1 + iv2
f1_iv
0.74260758278924621
  • 特征2的IV值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
yi = xy[(xy['f2']==0) & (xy['class']==1)].shape[0]
ni = xy[(xy['f2']==0) & (xy['class']==0)].shape[0]
iv0 = cal_iv(yi, yt, ni, nt)

yi = xy[(xy['f2']==1) & (xy['class']==1)].shape[0]
ni = xy[(xy['f2']==1) & (xy['class']==0)].shape[0]
iv1 = cal_iv(yi, yt, ni, nt)

yi = xy[(xy['f2']==2) & (xy['class']==1)].shape[0]
ni = xy[(xy['f2']==2) & (xy['class']==0)].shape[0]
iv2 = cal_iv(yi, yt, ni, nt)

f1_iv = iv0 + iv1 + iv2
f1_iv
2.1043458049450106

  从上面的结果可以看出，在这样的分箱下，特征0的预测效果最好，特征1的预测效果最差。当然，iv值的大小很大程度上也取决于我们是怎么对连续变量进行分箱的。

enjoy it!

可参考资料：
http://blog.csdn.net/qq_16365849/article/details/67632666
http://blog.csdn.net/qq_16365849/article/details/67632776

0%