HMM简介与实战

发表于

  有差不多3个星期没有更新博客了，清明假期回了趟江西也是把我堵怕了。不过这段时间也抽空回顾了下隐马尔可夫（HMM），同时动手写了下算法，今天总算是整理地差不多了。
  隐马尔可夫（HMM）模型描是一个关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。下面来回顾一下吧！

  隐马尔可夫（hidden Markov model）模型描是一个关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。在写这篇博客的过程中，知乎上的相关问题提供了很多通俗易懂的讲解。可以参考知乎。
  这里，我们先从一个直观的例子入手，了解一下隐马尔可夫的过程；然后从概念上进行一些解释；最后写代码进行实现。

先举个栗子

  作为一个吃鸡玩家，就围绕吃鸡举个栗子吧。我们利用地图副本的天气状况（状态变量）、第一局随机到地图天气的概率（初始状态概率）和我们的最后取得的成绩（观测变量）构建一个HMM。
  在这个模型中，假设地图天气状况3种，分别是晴天、黄昏和雨天（实际中已取消）。我们开始玩第一局的时候随机到每种天气的概率为（0.4,0.4,0.2），而接下来每局比赛的天气转换概率如图所示，比如这局是晴天，那么下局是晴天、黄昏、雨天的概率分别为0.5、0.3和0.2。而由于天气的不同，我们吃鸡队的游戏竞技状态也会有所变化，我们取得的成绩也就不一样。

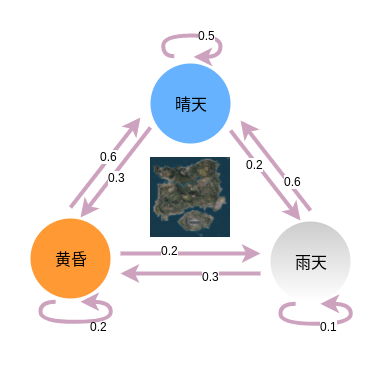
  比如，我们比较擅长晴天，打进前10、10-20和20以后的概率分别为0.6、0.3、0.1；黄昏天由于光线原因，打进前10、10-20和20以后的概率分别为0.3、0.5、0.2；而雨天由于视野和雨点噪声影响，打进前10、10-20和20以后的概率分别为0.2、0.5、0.3。
  根据上面的信息，我们其实可以得到HMM的一些基本要素，初始状态分布 $\pi$ 、状态转移分布 $A$、观测概率分布 $B$。
  3位朋友听说了我和队友今天在吃鸡，分别提出3个问题：

  • 1.朋友A已知了HMM模型的参数，了解到我们连续5局的成绩分别是：（5,10,23,15,1），他希望计算出我们打出这个成绩的概率是多少；
  • 2.朋友B只知道我们连续5局的成绩，他希望估计出HMM模型的三个参数 $(\pi,A,B)$;
  • 3.朋友C已知了HMM模型的参数和我们连续5局的成绩，她希望能猜测出这5局的地图天气分别是什么；

  最后一局终于吃鸡，上张吃鸡图。

基本概念

  HMM模型由初始状态概率向量 $\pi$ 、状态转移矩阵 $A$、观测概率矩阵 $B$ 组成。$\pi$ 和 $A$ 决定了状态序列，$B$ 决定了观测序列，这三个参数称为HMM的三要素。
  可以看出来，HMM做了两个基本假设：

  • 1.齐次马尔可夫性假设：隐藏的马尔可夫链在任意时刻 $t$ 的状态只依赖于前一时刻的状态，与其他时刻的状态及观测无关；
  • 2.观测独立性假设：即任意时刻的观测只依赖与该时刻的马尔可夫链的状态，与其他观测及状态无关；

  HMM模型的三个基本问题是：

  • 1.概率计算问题：给定模型 $(\pi,A,B)$ 和观测序列 $(o_{1},o_{2},…,o_{T})$，计算在这个模型参数下得到该序列的概率；即吃鸡例子中该出这个成绩的概率是多少？
  • 2.学习问题：已知出现的观测序列 $O=(o_{1},o_{2},…,o_{T})$，估计模型参数 $\lambda=(\pi,A,B)$，使得在该模型下观测序列的概率 $P(O|\lambda)$ 最大。不知道大家有没有发现，这其实就是一个可以运用EM算法解决的场景;即吃鸡例子中希望估计的模型参数；
  • 3.预测问题：也成为解码问题，已知模型参数 $\lambda=(\pi,A,B)$ 和观测序列 $O=(o_{1},o_{2},…,o_{T})$，求对给定观测序列条件概率 $P(O|\lambda)$ 最大的状态序列 $I=（i_{1},i_{2},…,i_{T}）$，就是说给定观测序列，求最有可能对应的状态序列；即吃鸡例子中预测处5局的天气分别是什么。

问题解法

概率计算问题

  对于这个问题，依照齐次马尔可夫性假设，我们可以按照实际观测罗列出所有的状态路径，然后求各个状态与观测序列的联合概率，最后对所有可能的状态序列求和，得到条件概率 $P(O|\lambda)$。但是我们可以想想到的是，当状态维度、时序长度增大时，这个方法的计算量是很大的，有 $O(NT^{N})$ 阶，是不可行的。下面简单介绍下实际可行的前向-后向算法。

  首先讲前向算法

给定HMM的 $\lambda$，定义到时刻t部分的观测序列为 $o_{1},o_{2},…,o_{t}$ 且状态为 $q_{i}$ 的概率为前向概率，记作 $\alpha_{t}(i)=P(o_{1},…,o_{t},i_{t}=q_{i} \ | \ \lambda) $。

  现在我们知道5局的成绩是（5,10,23,15,1），先计算第1局获得前10成绩的概率，如果是晴天，根据条件概率则

  如果是黄昏，则

  如果是雨天，则

  接下来计算第2局时获得前10的概率，首先如果第2局是晴天，那么：

  如果第2局是黄昏，那么：

  同样如果第2局是雨天，那么：

  如此下去可以继续计算第3局的情况。可以看出，前向算法计算了每个时间点，每个状态的发生观测序列的概率，在观测时序长度增大时，复杂度会大大降低。前向算法的公式可以参见《统计学习方法》中的P175。算法过程如下图：


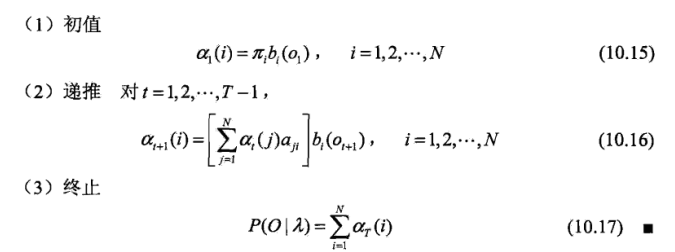
  与前向算法不同，后向算法则是倒退着，从最后一个状态开始慢慢往后推。

给定HMM的 $\lambda$，定义在时刻 $t$ 状态为 $q_{i}$ 的条件下，从 $t+1$ 到 $T$ 部分的观测序列为 $o_{t+1},…,o_{T}$ 的概率为后向概率，记作 $\beta_{t}(i)=P(o_{t+1},…,o_{T} \ | \ i_{t}=q_{i},\lambda)$

  假设观测序列长为 $T$，后向算法为 $\beta_{T}(i)=1$，这是因为 $T$ 后没有观测值了。那么在第4局游戏中天气为黄昏的状态下，第5局前10的后向概率可以计算为：

  后向算法的公式可以参见《统计学习方法》中的P178。算法过程如下图：

  利用前向概率和后向概率的定义，可以将观测序列概率 $P(O|\lambda)$ 统一写为：

参数学习问题

  对HMM模型的参数学习问题本质上是一个存在隐变量的参数估计问题，可以用非监督学习算法Baum-Welch算法（也就是EM算法）来做。具体的过程博主并未实际推导，求得的结果参数可以参考《统计学习方法中》的10.3.3章节的三个式子。

预测问题

  HMM可以使用维特比算法来进行状态预测。维特比算法实际是用动态规划解HMM模型预测问题，即用动态规划求概率最大的路径，这个时候的一条路径就对应一个状态序列。
  对于已知的模型参数 $\lambda=(A,B,\pi)$ 和观测 $O=o_{1},…,o_{T}$，维特比算法的步骤是：

  • 1.初始化
  • 2.递推，对于 $t=2,3,…,T$，有
  • 3.终止
  • 4.最优路径回溯，对于t=T-1,…,1，求得最优路径 $I^{}=(i_{1}^{},…,i_{T}^{*})$。

代码实现

  以下代码是按照《统计学习方法》中的算法步骤实现的，代码对应的公式也有注释。注：隐状态预测代码待补充。

1
2
3
4
5
import numpy as np
import random

state_dict = {0: '晴天', 1: '黄昏', 2: '雨天'}
observe_dict = {0: '前10名', 2: '10-20名', 3: '20名以后'}

  定义HMM类，包括了上述的三种问题求解的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
class HMM(object):
    def __init__(self, n_state_=None, run_type_='probability', m_observe_=None,
                 state_transfer_=None, observe_prob_=None, start_prob_=None, observe_=None, max_step=100):
        # 概率计算问题
        if run_type_ == 'probability':
            if n_state_ is None or state_transfer_ is None or start_prob_ is None or observe_prob_ is None or m_observe_ is None or observe_ is None:
                raise ValueError('missing parameter for HMM {}'.format(run_type_))
            self.observe_prob = observe_prob_
            self.n_state = n_state_
            self.m_observe = m_observe_
            self.state_transfer = state_transfer_
            self.start_prob = start_prob_
            self.observe = observe_
        # 参数学习问题
        elif run_type_ == 'learning':
            if m_observe_ is None or n_state_ is None or observe_ is None:
                raise ValueError('missing parameter for HMM {}'.format(run_type_))
            self.n_state = n_state_
            self.m_observe = m_observe_
            self.observe = observe_
            self.max_step = max_step
            self.parameter_init()
        # 预测问题
        else:
            if n_state_ is None or state_transfer_ is None or start_prob_ is None or observe_prob_ is None or observe_ is None:
                raise ValueError('missing parameter for HMM {}'.format(run_type_))
            self.observe_prob = observe_prob_
            self.n_state = n_state_
            self.state_transfer = state_transfer_
            self.start_prob = start_prob_
            self.observe = observe_

    # 前向算法
    def forward(self):
        self.T = len(self.observe)
        self.alpha = np.matrix(np.zeros((self.T, self.n_state)))

        # step1 初值，对应公式 10.15
        prob = self.observe_prob[:, self.observe[0]]
        self.alpha[0] = self.start_prob * prob.T.getA()

        # step2 递推，对应公式 10.16
        for t in range(1, self.T):
            tmp1 = self.observe_prob[:, self.observe[t]].T.getA()
            tmp2 = (self.alpha[t-1] * self.state_transfer).getA()
            self.alpha[t] = tmp1 * tmp2

    # 后向算法
    def backward(self):
        self.beta = np.matrix(np.zeros((self.T, self.n_state)))

        # step1 初始化T时刻的后向概率为1，公式 10.19
        self.beta[-1] = np.ones((1, self.n_state))

        # step2 公式 10.20
        for t in range(self.T - 1):
            for i in range(self.n_state):
                sum_ = 0
                for j in range(self.n_state):
                    tmp1 = self.state_transfer[i, j]
                    tmp2 = self.observe_prob[j, self.observe[self.T - 1 - t]]
                    tmp3 = self.beta[self.T - 1 - t, j]
                    sum_ += tmp1 * tmp2 * tmp3
                self.beta[self.T - 1 - 1 - t, i] = sum_

    # 初始化HMM模型参数，用于参数估计
    def parameter_init(self):
        # 初始状态向量
        self.start_prob = np.array([1.0 / n_state] * self.n_state)
        # 状态转移概率矩阵
        self.state_transfer = np.matrix(np.zeros((self.n_state, self.n_state)))
        # 观测概率矩阵
        self.observe_prob = np.matrix(np.zeros((self.n_state, self.m_observe)))

        for i in range(self.n_state):
            random_list = [random.randint(0, 100) for t in range(self.n_state)]
            sum_ = sum(random_list)
            for j in range(self.n_state):
                self.state_transfer[i, j] = random_list[j] / sum_

        for i in range(self.n_state):
            random_list = [random.randint(0, 100) for t in range(self.m_observe)]
            sum_ = sum(random_list)
            for j in range(self.m_observe):
                self.observe_prob[i, j] = random_list[j] / sum_

    # 学习问题：估计模型参数
    def learning_parameters(self):
        print('learning')
        self.T = len(self.observe)

        step = 1
        while step < self.max_step + 1:
            print('step: {}'.format(step))
            step += 1

            # 计算前向后向概率
            self.forward()
            self.backward()

            # 计算期望值
            self.cal_gamma()
            self.cal_xi()

            # EM算法估计参数
            tmp_state_transfer = self.cal_state_transfer()
            tmp_observe_prob = self.cal_observe_prob()
            tmp_start_prob = self.cal_start_prob()

            self.state_transfer = tmp_state_transfer
            self.observe_prob = tmp_observe_prob
            self.start_prob = tmp_start_prob

        print('learning done')

    # 给定模型初始状态概率和观测序列，计算t时刻处于状态i的概率，公式10.24
    def cal_gamma(self):
        self.gamma = np.zeros((self.T, self.n_state))

        for t in range(self.T):
            p_full = np.dot(self.alpha[t], self.beta[t].T)[0, 0]
            p = self.alpha[t].getA() * self.beta[t].getA()
            self.gamma[t] = p / p_full

    # 给定模型初始状态概率和观测序列，计算t时刻处于状态i且t+1时刻处于状态j的概率，公式10.26
    def cal_xi(self):
        self.xi = np.zeros((self.T-1, self.n_state, self.n_state))
        p_full = np.zeros(self.T-1)

        for t in range(self.T-1):
            sum_ = 0
            for i in range(self.n_state):
                for j in range(self.n_state):
                    sum_ += self.alpha[t, i] * self.state_transfer[i, j] * \
                            self.observe_prob[j, self.observe[t+1]] * self.beta[t+1, j]
            p_full[t] = sum_

        for t in range(self.T-1):
            for i in range(self.n_state):
                for j in range(self.n_state):
                    p = self.alpha[t, i] * self.state_transfer[i, j] * \
                        self.observe_prob[j, self.observe[t+1]] * self.beta[t+1, j]
                    self.xi[t][i][j] = p / p_full[t]

    # EM算法计算状态转移矩阵
    def cal_state_transfer(self):
        tmp_state_transfer = np.matrix(np.zeros((self.n_state, self.n_state)))
        for i in range(self.n_state):
            sum_2 = self.gamma[:self.T - 1, i].sum()
            for j in range(self.n_state):
                sum_1 = self.xi[:, i, j].sum()
                tmp_state_transfer[i, j] = sum_1 / sum_2
        return tmp_state_transfer

    # EM算法计算观测概率矩阵
    def cal_observe_prob(self):
        tmp_observe_prob = np.matrix(np.zeros((self.n_state, self.m_observe)))
        for i in range(self.n_state):
            for k in range(self.m_observe):
                sum_1 = 0
                sum_2 = 0
                for t in range(self.T):
                    if k == self.observe[t]:
                        sum_1 += self.gamma[t, i]
                    sum_2 += self.gamma[t, i]
                tmp_observe_prob[i, k] = sum_1 / sum_2
        return tmp_observe_prob

    # EM算法计算初始概率向量
    def cal_start_prob(self):
        return self.gamma[0, :]

    # 状态预测算法，维特比算法，后续补充
    def predict_state(self):
        pass

  概率计算问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 定义状态转移矩阵，即地图三种天气的状态转换
state_transfer = np.matrix([[0.5, 0.3, 0.2],
                            [0.6, 0.2, 0.2],
                            [0.6, 0.3, 0.1]])

# 定义观测概率矩阵，即地图三种天气状态对应的观测概率
observe_prob = np.matrix([[0.6, 0.3, 0.1], [0.3, 0.5, 0.2], [0.2, 0.5, 0.3]])
# 状态数
n_state = 3
# 观测数
m_observe = 3
# 起始状态分布向量
start_prob = np.array([0.4, 0.4, 0.2])
# 观测序列，即连续5局的战绩[前10，前10，20开外，10-20，前10]
observe = [0, 0, 2, 1, 0]
hmm = HMM(observe_prob_=observe_prob, n_state_=n_state,
          m_observe_=m_observe, state_transfer_=state_transfer,
          start_prob_=start_prob, observe_=observe)
# 前向概率计算
hmm.forward()
# 后向概率计算
hmm.backward()

forward_p = hmm.alpha[-1].sum()
backward_p = 0
for i in range(n_state):
    backward_p += hmm.start_prob[i] * hmm.observe_prob[i, observe[0]] * hmm.beta[0, i]

print('前向概率： {}'.format(forward_p))
print('后向概率： {}'.format(backward_p))
前向概率： 0.005115324
后向概率： 0.005115324

  参数学习问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
observe = [0, 1, 2, 2, 1, 1, 0, 2, 1]
n_state = 3
m_observe = 3
hmm = HMM(n_state_=n_state, m_observe_=m_observe,
          run_type_='learning', observe_=observe,
          max_step=10)
hmm.learning_parameters()

print('初始状态概率向量：')
print(hmm.start_prob)
print('状态转移矩阵：')
print(hmm.state_transfer)
print('观测概率矩阵：')
print(hmm.observe_prob)
learning
step: 1
step: 2
step: 3
step: 4
step: 5
step: 6
step: 7
step: 8
step: 9
step: 10
learning done
初始状态概率向量：
[1.49529045e-05 9.99985047e-01 5.03432572e-13]
状态转移矩阵：
[[1.91880239e-01 5.57882397e-05 8.08063973e-01]
 [1.70532635e-03 1.76861116e-13 9.98294674e-01]
 [1.68273868e-01 1.19887600e-01 7.11838432e-01]]
观测概率矩阵：
[[2.85459304e-01 7.25724096e-02 6.41968286e-01]
 [9.99774837e-01 3.54499362e-05 1.89713434e-04]
 [8.22150576e-03 6.25644638e-01 3.66133857e-01]]

enjoy it!

参考资料：https://www.zhihu.com/question/20962240

0%