今天来回顾一下EM算法。试想,当通过若干次实验获取一批硬币观测数据时,如果知道他们分别来自哪个硬币,我们就可以通过极大似然估计来求得其每个硬币分布的参数。但是,如果我们不知道他们来自哪个分布(称作隐变量)的时候,极大似然估计方法就失效了。EM(expectation maximization)算法就是针对这样有隐变量的参数估计场景。这篇博文里,我们不谈数学推理公式,通过简单的例子了解一下EM算法的idea。
另外,临近春节,在这里预祝大家新年快乐啦!
EM算法浅析
EM算法回顾
EM算法(expectation maximization algorithm)是一种迭代算法,用于含有隐变量的概率模型参数的最大似然估计,或极大后验概率估计。
EM算法的每次迭代由两步组成:
- E步,求期望;
- M步,求极大;
概率模型有时既有观测变量,又含有隐变量或潜在变量。如果概率模型所有的变量都是观测变量,那么给定数据,就可以使用最大似然估计法,或贝叶斯法估计模型参数(最大似然和贝叶斯的区别我们稍后讲)。但是,当模型含有隐变量时,就不能简单得使用这些估计方法。EM算法就是含有隐变量的概率模型的最大似然估计方法,或极大后延概率估计方法。
举个栗子
我们先抛开数学公式,从例子入手,先对EM算法有一个直观的认识。博主认为,理解一个方法背后的idea是最重要的。
假设做一个硬币实验,我们有两个硬币,每个硬币有正面反面,其参数我们不得而知。我们假设 $\theta_{A}$ 和 $\theta_{B}$ 分别为A、B硬币的正面概率,则 $1-\theta_{A}$ 和 $\theta_{B}$ 分别为A、B硬币的反面概率。现在我们做5次实验,每次实验从A、B中选择一个,抛掷10次。
忘记了什么是最大似然的同学可以在这里回想一下。
什么是似然,似然就是给了我们一堆的随机实验结果x,我们知道其分布,但是不知道其分布的参数 $\theta$ ,我们需要通过x来推测分布的参数 $\theta$ 。那么,我们怎么通过最大似然方法来推测出分布的参数呢?每一次实验结果我们可以写成 $P(x_{i}|\theta)$ ,即在某参数的分布下,发生这次结果的概率,每一次实验结果都是独立事件,所以多个实验就可以写成 $\prod_{i=1}^{n} P(x_{i}|\theta)$ 。这些结果是从分布中随机发生的,那么既然发生了,为什么不让出现的结果的可能性最大呢?这就是最大似然估计的核心。
无隐参数,最大似然估计
如果我们知道5次实验中每次选择了哪个,那么我们就知道了所有的观测变量,我们就可以使用最大似然估计的方法来推测分布的参数,实验如下图所示。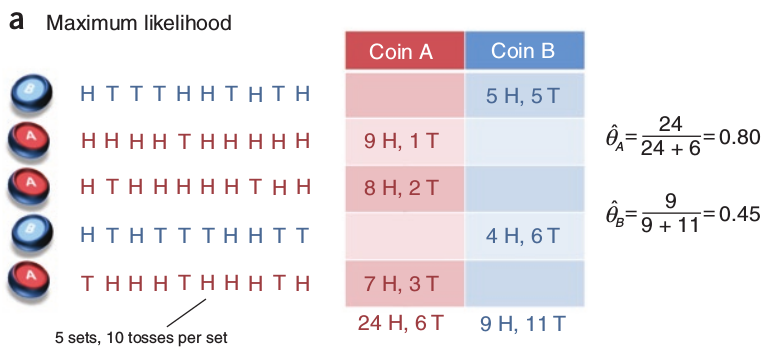
我们可以知道,第1、4次中是按硬币B的分布进行实验,第2、3和5次中是按硬币A的分布进行实验的。那么,通过最大似然估计方法,我们可以计算两个分布的推测参数出 $\hat{\theta_{A}}=0.80$ 和 $\hat{\theta_{B}}=0.45$ 。
有隐参数z,EM
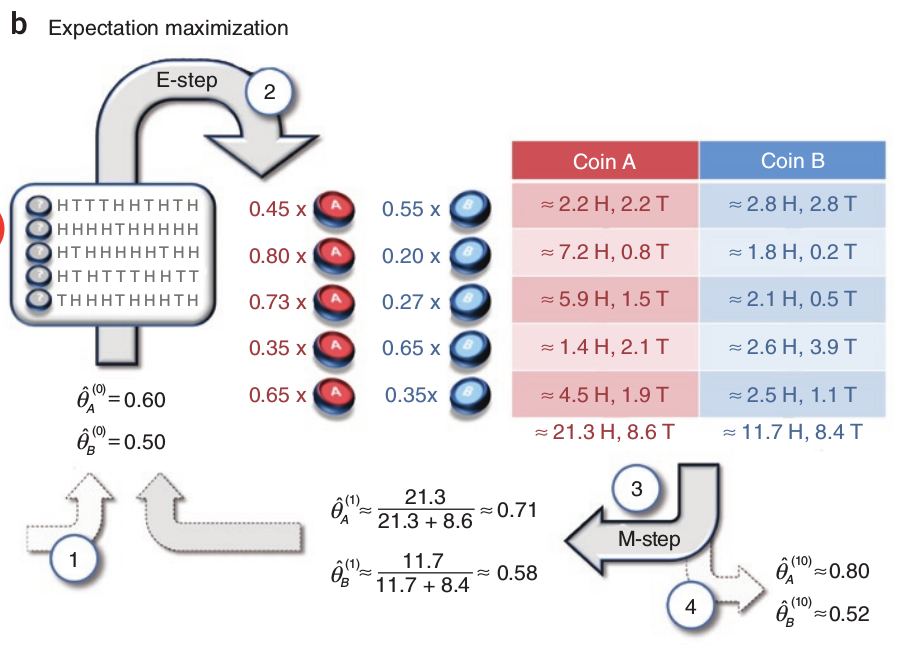
初始版
这次,我们不知道5次实验中每次是挑选了哪枚硬币,每次实验所挑选出来的硬币我们称其为隐变量z,这是一个不完全数据的情况,我们无法通过最大似然估计来求出分布的参数。
一个可行的想法是做一下的迭代,我们先初始化分布A、B两个硬币的参数 $\hat{\theta}^{t}=(\hat{\theta}_{A}^{t},\hat{\theta}_{B}^{t})$ ,然后计算每轮投掷中,A、B各自出现的概率,并将概率大的作为本次迭代中该轮选择的硬币。以上图为例:假设初始分布为 $(\hat{\theta}_{A}^{1}=0.6,\hat{\theta}_{B}^{1}=0.5)$ ,根据第一次实验出现的观测,A硬币出现这样的概率为:
1 | p1a = pow(0.6, 9) * pow(0.4, 1) |
0.004031078399999999
B硬币出现这样的概率为:
1 | p1b = pow(0.5, 5) * pow(0.5, 5) |
0.0009765625
显然A出现这样的观测数据的可能性更大,所以可以把第一次实验选择的硬币暂定为A。每次实验分别按照上述方法进行计算,可以得到硬币选择预测结果,
| 试验轮次 | A硬币 | B硬币 |
|---|---|---|
| 1 | 0.000796 | 0.0009765 |
| 2 | 0.004031 | 0.0009765 |
| 3 | 0.002687 | 0.0009765 |
| 4 | 0.0005308 | 0.0009765 |
| 5 | 0.001792 | 0.0009765 |
选择可能性最大的值,结果依次为:BAABA。相当于我们求出了本轮迭代的隐变量。接下来,通过求出的隐变量,我们利用最大似然估计方法估计出下一轮的分布参数:
继续迭代下去直到分布的参数不变或变动极小。
需要注意的是,这个方法并不一定能收敛到真实的分布参数,这跟初始值的设定是有关系的。
实际上,EM算法就是基于这样的思想来的。相比上面的按照观测数据直接判断某次实验的隐变量,我们可以使用更加折中的方法,EM算法计算隐参数中每个取值的概率值。我们看下上面方法的升级版。
升级版
上面初始版中,我们用最大似然方法确定了隐变量z,然后再迭代估计新的分布参数。也就是说,我们在每轮中,选择了可能性最大的z值,而不是所有可能的z值。我们会看一下刚刚第一次迭代中估算出隐参数的概率,
| 试验轮次 | A硬币 | B硬币 |
|---|---|---|
| 1 | 0.000796 | 0.0009765 |
| 2 | 0.004031 | 0.0009765 |
| 3 | 0.002687 | 0.0009765 |
| 4 | 0.0005308 | 0.0009765 |
| 5 | 0.001792 | 0.0009765 |
根据上表,我们可以转换成A硬币和B硬币发生的概率,
| 试验轮次 | A硬币 | B硬币 |
|---|---|---|
| 1 | 0.45 | 0.55 |
| 2 | 0.80 | 0.20 |
| 3 | 0.73 | 0.27 |
| 4 | 0.35 | 0.65 |
| 5 | 0.65 | 0.35 |
实际上,上表表示的是期望值。以第一行为例,从期望角度看,本次试验使用硬币B的概率是0.55,相比初始版本,我们按照最大似然概率,将本次试验直接估计为B硬币,这里显得更加谨慎,仅表示有0.55的概率是硬币B。所以这一步,我们是估计了隐参数z的概率分布,也就是E步。
接下来,我们根据隐参数的期望,继续使用最大似然估计的方法估计A和B分布的参数。以第一次试验为例,出现了5次正面,5次反面,对于硬币A相当于 正面为$0.45*5=2.25$,反面为$0.45*5=2.25$;对于硬币B相当于正面为$0.55*5=2.75$,反面为 $0.55*5=2.75$。五次试验的结果如下表,
| 试验轮次 | A硬币 | B硬币 |
|---|---|---|
| 1 | 2.25正,2.25反 | 2.75正,2.75反 |
| 2 | 7.2正,0.8反 | 1.8正,0.2反 |
| 3 | 5.9正,1.5反 | 2.1正,0.5反 |
| 4 | 1.4正,2.1反 | 2.6正,3.9反 |
| 5 | 4.5正,1.9反 | 2.5正,1.1反 |
| 合计 | 21.3正,8.6反 | 11.7正,8.4反 |
接下来,根据最大似然方法可以估计本轮之后,硬币A和B的参数为$\hat{\theta}_{A}^{2}=0.71,\hat{\theta}_{B}^{2}=0.58$。这一步也就是M步。接下来,可以进行下一轮的迭代…
总结一下
通过上面那个例子,我们可以体会到EM算法思想的精彩之处,直观得感觉到背后的idea。以上就是EM算法浅析,有机会深入学习一下背后的推理思维,与大家一起分享。
