boosting提升算法是一种把若干个分类器整合为一个分类器的方法。在监督学习中，它可以很好的降低bias和variance。它将若干弱分类器组合成一个强分类器。可谓“三个臭皮匠，顶个诸葛亮”。

提升方法

boosting提升方法是常用的统计学习方法。在分类问题中，它通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。这里我们主要看一下AdaBoost，和提升树boosting tree模型，还有xgboost的内容。理解程度可能不深，如果所述之处如有错误，还请指出。

AdaBoost

基本思路

提升方法的思想是，对于一个复杂的任务，多个判断进行综合后的结果，会比单个判断效果要好，就像是“三个臭皮匠定个诸葛亮”的道理。
对于分类问题来说，给定一个训练集后，求出一个较为粗糙的分类规则要比求出一个精确的分类规则要容易的多。提升方法从弱学习算法出发，反复学习，得到一系列弱分类器，然后组合这些弱分类器，构成一个强分类器。AdaBoost是改变训练数据的概率分布（训练数据的权值分布），针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。

算法

假设有一个二分类的训练集： $T=\{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})\}$
其中，$y_{i} \in Y=\{-1,+1\}$
AdaBoost利用一下算法，从训练集中学习一系列弱分类器，并将这些弱分类器组合成为一个强分类器。

对算法的步骤我们进行一下简单分析：

初始时，训练集每个样本的均分布的，训练数据的权值都是$\frac{1}{N}$；
每一轮的分类误差率$e_{m}$用公式8.1计算，其中$I（true）$等于1；
总结一下，AdaBoost在每一轮的学习过程中，训练步骤为：

使用当前权值概率分布从训练集中进行采样，学习基本分类器$G_{m}(x)$，m为第m次轮；
计算基本分类器$G_{m}(x)$在采样后训练集上的分类误差率:

$e_{m}=P(G_{m}(x_{i} \neq y_{i}))=\sum_{G_{m}(x_{i} \neq y_{i})} \omega_{mi}$

$\omega_{mi}$表示第m轮中第i个示例的权值，$\sum_{i=1}^{N} \omega_{mi}=1$；

计算基本分类器$G_{m}(x)$的系数$\alpha_{m}$，表示$G_{m}(x)$在最终分类器中的重要性；
计算规范化因子，使得$D_{m+1}$成为一个概率分布， $Z_{m}=\sum_{m=1}^{N} \omega_{mi} \exp(-\alpha_{m}y_{i}G_{m}(x_{i}))$
更新训练数据集的权值分布 $\omega_{m+1,i}=\begin{cases}\frac{\omega_{mi}}{Z_{m}}e^{-\alpha_{m}},G_{m}(x_{i})=y_{i}\\&&&&\\\frac{\omega_{mi}}{Z_{m}}e^{\alpha_{m}},G_{m}(x_{i}) \neq y_{i}\end{cases}$ 可以看到，被基本分类器误分类的样本权值得以扩大，被正确分类样本的权值得以缩小。因此，误分类的样本将在下一轮的学习中起更大的作用；

注意，基本分类器在学习新的分布数据的时候，数据的权值怎么体现出来呢？答案是，每个数据的分布权值体现在损失函数中。
最终分类器实现M个基本分类器的加权表决，系数$\alpha_{m}$表示基本分类器$G_{m}(x)$的重要性，需要注意的是，$\alpha_{m}$的和并不为1； $G(x)=sign(f(x))=sign(\sum_{m=1}^{M} \alpha_{m}G_{m}(x))$
《统计学习方法》中提供了一个简单的例子，可以参看P140下例8.1

AdaBoost算法的解释

前向分步算法

加法模型可以用公式表示为： $f(x)=\sum_{m=1}^{M} \beta_{m}b(x;\gamma_{m})$
其中，$b(x;\gamma_{m})$是基函数，$\gamma_{m}$为基函数参数，$\beta_{m}$为基函数系数；
给定数据集和损失函数的条件下，加法模型$f(x)$的损失函数极小化问题就变成： $\min_{\beta_{m},\gamma_{m}} \sum_{i=1}^{N} L(y_{i},\sum_{m=1}^{M}\beta_{m}b(x_{i};\gamma_{m}))$
但这是一个复杂的优化问题，前项分步算法的解决思路是：从前向后，每一步值学习一个基函数及其系数，逐步逼近优化目标函数，具体的，每一步只需要优化如下损失函数： $\min_{\beta,\gamma} \sum_{i=1}^{N} L(y_{i},\beta b(x_{i};\gamma))$
算法如下：

提升树

提升树方法实际就是采用加法模型和前向分步算法。我们称以决策树为基函数的提升方法为提升树（boosting tree）。提升树模型可以表示为决策树的加法模型：

$f_{M}(x)=\sum_{m=1}^{M}T(x;\Theta_{m})$

其中，$T(x;\Theta_{m})$ 表示一决策树，$\Theta_{m}$ 是决策树的参数，$M$ 表示树的个数。

提升树算法

首先确定初始提升树 $f_{0}(x)=0$ ，第m步的模型为：

$f_{m}(x)=f_{m-1}(x)+T(x;\Theta_{m})$

其中 $f_{m-1}(x)$ 是当前模型，通过经验风险极小化确定下一棵决策树的参数：

$\hat{\Theta}_{m}=\arg\min_{\Theta_{m}}\sum_{i=1}^{N}L\big(y_{i},f_{m-1}(x)+T(x;\Theta_{m})\big)$

下面讨论回归问题的决策树，假设训练集$T=\{(x_{1},y_{1}),…,(x_{N},y_{N})\},x_{i} \in \gamma \subseteq R^{n}$，$\gamma$是输入空间。如果将输入空间划分为J个互不相交的区域$R_{1},R_{2},…,R_{J}$，并且在每个区域上确定输出的常量$c_{j}$，那么树可以表示为：

$T(x;\Theta)=\sum_{j=1}^{J}c_{j}I(x \in R_{j})$

参数可以看做集合 $\Theta=\{(R_{1},c_{1}),…,(R_{j},c_{j})\}$ 表示树的区域划分和个区域上的常数。J是回归树的复杂度即叶节点的个数。
在前向分步算法的第m步，给定当前模型$f_{m-1}(x)$，需要求解 $\hat{\Theta}_{m}$，即第m棵树的参数。
如果我们采用平方误差作为损失函数：

$L(y,f(x))=(y-f(x))^{2}$

即

$L(y,f_{m-1}(x)+T(x;\Theta_{m}))=[y-f_{m}(x)-T(x;\Theta_{m})]^{2}=[r-T(x;\Theta_{m})]^{2}$

其中 $r=y-f_{m-1}(x)$，被称为提升树拟合数据的残差。回归问题的提升树算法如下：

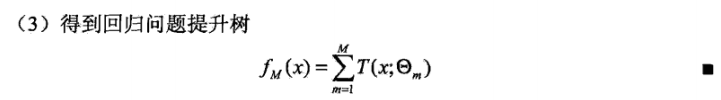
书中P149的例8.2很好的实现了这个算法过程。

梯度提升树（GBDT）

提升树利用加法模型和前向分步算法实现学习的优化过程。当损失函数是平方损失函数MSE时，每一步的优化很简单。但是对于一般损失函数来说，每一步的优化就没那么容易。使用梯度提升算法可以解决这个问题，利用损失函数的负梯度在当前模型的值

$-\bigg[\frac{\partial L(y,f(x_{i}))}{\partial f(x_{i})} \bigg ]_{f(x)=f_{m-1}(x)}$

作为回归问题提升树算法中的残差近似值，拟合一个回归树，这就是梯度提升。可以看到当损失函数为$L(y,f(x))=\frac{1}{2}(y-f(x))^{2}$时，计算的负梯度结果恰好是残差值 $y-f_{m-1}(x)$
梯度提升算法过程如下：

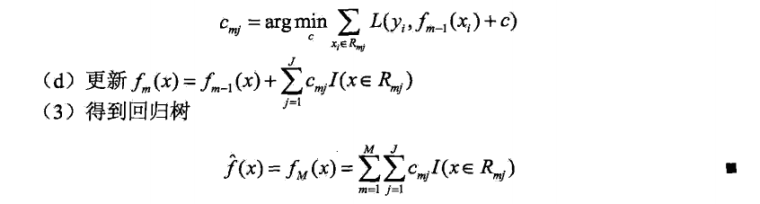
算法详解：第1步初始化，估计使损失函数极小化的常数值，它是只是有一个根节点的树；第2(a)步计算损失函数的负梯度在当前模型的值，将它作为残差的估计；第2(b)步估计回归树每个叶节点的区域，以残差近似值拟合一棵树（通常是CART）；第2(c)步利用线性搜索估计叶节点区域的值，使损失函数极小化（这里有一点容易产生疑惑的是，在2(b)拟合出决策树后，每个叶节点区域$R_{mj}$上已经有对应的取值，即归入了该区域的样本的均值，为什么还会有2(c)中求解叶节点区域的值呢？我们稍后再看）；第2(d)步更新回归树；第3步得到输出的最终模型 $\hat{f}_{(x)}$

关于上面的疑惑，查找资料可以发现这是一个改进后的梯度提升方法（TreeBoost），先看一下原始的方法如下图：

原始方法中，在以残差近似值拟合出一棵树后，每个区域$R_{jm}$都会有个对应的取值$b_{jm}$，同时这棵树会有一个系数$\gamma_{m}$，$\gamma_{m}$的值通过2.3步的方法求解。
改进的方法如下图，取代一棵树一个系数值，对于每一棵树的每个区域$R_{jm}$都求得一个对应的系数值，系数的求解方法就是上面中文算法流程中的2(c)步骤。

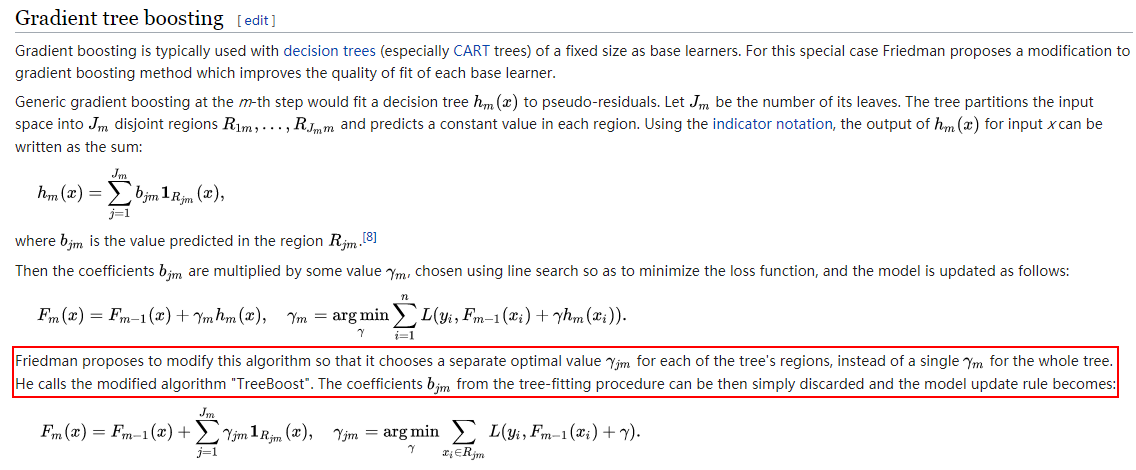
截图来源：https://en.wikipedia.org/wiki/Gradient_boosting

XGBoost

xgboost是华盛顿大学陈天奇大神团队的成果，这个算法在kaggle很多比赛中都取得了很好的效果，展现出了强大的性能。xgboost可以看做是gbdt的强化版本，相对gbdt有以下几点升级:

传统GBDT以CART作为基分类器，xgboost还支持线性分类器，这个时候xgboost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）；
传统GBDT在优化时只用到一阶导数信息，xgboost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。同时，xgboost工具支持自定义代价函数，只要函数可一阶和二阶求导；
xgboost在代价函数里加入了正则项，用于控制模型的复杂度；
Shrinkage（缩减），相当于学习速率（xgboost中的eta）。xgboost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间；
支持列抽样；
对缺失值的处理。对于特征的值有缺失的样本，xgboost可以自动学习出它的分裂方向；
支持并行;

Boosting提升方法