之前参加了《机器学习数学基石课程》,也是对毕业前学习的课程上做了些补充,这里回顾一下机器学习优化问题的知识点,很多内容来自课程PPT。
迭代统一论
无约束优化问题
自变量为标量的函数:
自变量为向量的函数:
优化问题可能的极值点情况
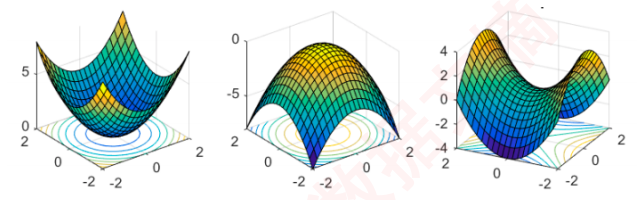
数学要点
一阶二阶导数

假设n维数据,x是一个向量,我们可以求得x的一阶导数,结果仍然是一个向量;对其求二阶导数,得到的是一个$n*n$的矩阵,这个矩阵被称为Hessian矩阵
二次型

二次型有什么用?
相对标量中的正数,二次型可以用来衡量矩阵A的“正负”
如果一个矩阵A的二次型大于等于0,称为半正定矩阵;大于0则称为正定矩阵;小于则称为负定矩阵;
具体计算如下:
泰勒级数

泰勒级数和极值求解有非常大的关联!
无约束优化梯度分析法
泰勒级数和极值
对于标量情况下,泰勒级数和极值的关系如下
结合上面的知识点,在向量情况下,泰勒级数和极值的关系如下
无约束优化迭代法
机器学习问题本质上是一个数学优化问题,我们定义了目标函数(损失函数)之后,想办法寻找损失函数的全局最小值或局部最小值,很多时候就是通过迭代求梯度、更新权值的方式寻找最优解。普遍的,无约束优化迭代法过程如下: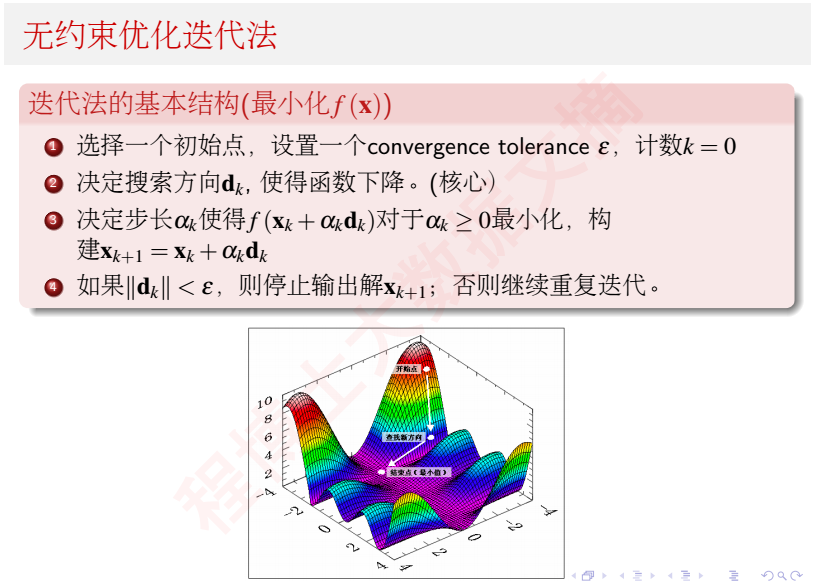
梯度下降法
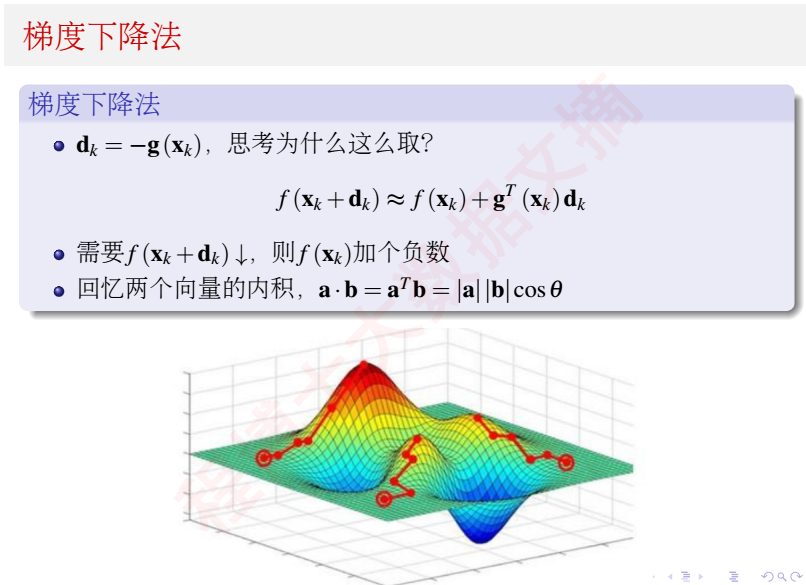
牛顿法
除了常见的梯度下降法,还有在数学层面上更加精准的牛顿法,牛顿法是求了目标函数的Hessian矩阵,下降方向的选取更加精准
但是牛顿法有其弱点,就是在实际的工程中,Hessian矩阵是很难解的,Hessain矩阵的逆就更难了,对此,可以用逆牛顿法来逼近牛顿法。
